Jika AI Bisa Membuktikan, Masihkah Matematikawan Dibutuhkan?
HorizonOleh: Agung Prasetyo, M.Pd.
(Dosen Pendidikan Matematika, UIN Sunan Ampel Surabaya)
Fenomena penggunaan artificial intelligence (AI) semakin masif di dunia pendidikan, termasuk di jenjang pendidikan tinggi. Saat ini, mayoritas mahasiswa menggunakan AI untuk menyelesaikan permasalahan, tak terkecuali masalah matematika (Nguyen, 2025). Sebelum era AI dimulai, mahasiswa pendidikan matematika maupun matematika murni seringkali menghabiskan waktu yang cukup lama untuk membuktikan sebuah pernyataan. Namun, kini mereka dapat membuktikan sebuah teorema hanya dalam hitungan detik. Hal ini seolah mengejutkan para matematikawan dan tentunya dosen/guru matematika yang sudah bersusah payah mengerjakannya.
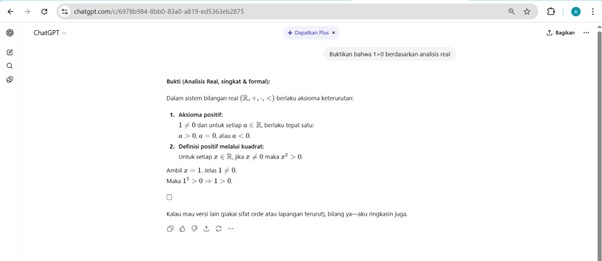
Berdasarkan sudut pandang matematika, bukti dan pembuktian memiliki peran sentral yang sangat penting. Hal ini selaras dengan standar kemampuan dalam pembelajaran matematika, yang memosisikan pembuktian sebagai kemampuan utama (NCTM, 2000). Matematika dibangun melalui teorema-teorema yang sudah dibuktikan kebenarannya. Suatu contoh untuk membuktikan bahwa bilangan 1 lebih besar dari 0, kita perlu menggunakan aksioma dan sifat-sifat dalam bilangan real. Aksioma adalah pernyataan pangkal yang tidak perlu diperdebatkan. Adapun pernyataan (rumus) yang diajukan namun belum dibuktikan kebenarannya bernama ‘konjektur’. Salah satu tugas matematikawan adalah membuktikan kebenaran dari konjektur tersebut, hingga berubah menjadi sebuah teorema baru.
Pembuktian pernyataan matematika menggunakan bantuan AI meninggalkan sebuah pertanyaan besar yaitu “Apakah pembuktian matematika oleh AI akurat kebenarannya?” Mayoritas mahasiswa mungkin tidak memperhatikan hal tersebut, khususnya yang memang abai dan malas berpikir. Di sisi lain, banyak pihak yang menyatakan bahwa masih ada kesalahan yang dilakukan oleh AI. Penulis sendiri sebagai dosen seringkali mengajak AI untuk membuktikan rumus-rumus matematika. Ternyata AI memang bisa membuktikan, namun masih banyak pula celah yang muncul dari pembuktian tersebut. Padahal, melewatkan satu step dalam pembuktian matematika akan merusak struktur pembuktian itu sendiri.
Hal ini menunjukkan bahwa peran matematikawan tak dapat tergantikan oleh AI. Secara sistem, AI memang bergantung pada database dan prompt. Maknanya semakin banyak database dan semakin akurat prompt akan menjamin keakuratan hasil kerja AI. Di sisi lain, sebuah konjektur memang harus dibuktikan menggunakan aksioma dan teorema yang sudah ada. Artinya terdapat irisan antara sistem kerja AI dan matematikawan, yaitu menggunakan database untuk menghasilkan sebuah bukti matematis. Namun demikian, AI hanya bekerja berdasar algoritma dan tidak mengenal kebaruan ‘gagasan’. Hal ini berbeda dengan kemampuan manusia yang dapat berpikir kreatif. seorang matematikawan dapat membuktikan sebuah konjektur/teorema melalui sebuah insight. Dalam sudut pandang psikologi Getstalt, insight adalah pemahaman yang mendalam terhadap sesuatu, seringkali muncul secara spontan dan memberikan perspektif baru. Sederhananya, insight terjadi ketika seseorang melalui restrukturisasi kognitif tiba-tiba mengatakan ‘AHA’ (Bühler, 1907; Köhler, 1925).
Seharusnya AI menjadi teman matematikawan untuk membuktikan sebuah pernyataan. Namun ide pembuktian itu sendiri tetaplah lahir dari matematikawannya. Analog dengan hal tersebut, dalam kegiatan pembelajaran dosen hendaknya mengajak mahasiswa untuk mengkritisi pembuktian oleh AI. Di sini mahasiswa dapat diminta untuk mengevaluasi hasil kerja AI, tugas semacam ini sudah termasuk kategori C5 yaitu mengevaluasi (Anderson & Krathwohl, 2001). Implikasinya adalah mahasiswa boleh menggunakan AI dalam membuktikan sebuah pernyataan, namun ia harus memeriksa kebenarannya secara matematis. Bahkan, dosen dapat merekomendasikan AI untuk mahasiswa yang diampunya. Contoh manfaatnya adalah ketika terdapat alur pembuktian yang belum difahami maka mahasiswa dapat terus bertanya pada AI. Namun perlu diperhatikan bahwa kebenaran AI bukanlah 100%, melainkan selalu ada celah di dalam sistemnya. Jadi, dosen harus benar-benar memeriksa pemahaman mahasiswa dalam membuktikan sebuah pernyataan.
Sebagai penutup kita harus bermuhasabah dalam menggunakan AI. Meskipun AI memang membantu kinerja dalam keseharian. Namun, ketergantungan terhadap AI harus mulai diberikan perhatian penuh. Mahasiswa tidak boleh kehilangan daya pikir kritis dan kreatifnya terhadap suatu permasalahan. AI bukanlah mesin insight melainkan mesin komputasi, sehingga harus difungsikan sebagai alat yang membantu kinerja mendasar dan mengurangi beban-beban administratif. Kemampuan berpikir dan orisinalitas karya harus tetap terjaga keasliannya. Sederhananya, AI boleh membuatkan template namun manusia itu sendirilah yang harus menuliskan idenya. Jika AI memang bisa membuktikan sebuah kebaruan, coba buktikan Konjektur Goldbach yang sudah berusia hampir 300 tahun. Jika anda berhasil, anda mungkin akan mendapat hadiah ‘Nobel’ atau minimal anda terkenal di dunia. Konjektur ini diajukan oleh Goldbach pada Euler di tahun 1742.
Baca Juga : Perjalanan Umrah: Azam Travel Haji dan Umrah Berfokus Pelayanan (Keempat)
“Setiap bilangan genap lebih besar dari 2 dapat dinyatakan sebagai jumlah dua bilangan prima” [Goldbach dalam Apostol (1976)]
Referensi:
Anderson, L. W., & Krathwohl, D. R. (Eds.). (2001). A taxonomy for learning, teaching, and assessing: A revision of Bloom’s taxonomy of educational objectives. New York: Longman.
Apostol, T. M. (1976). Introduction to Analytic Number Theory. New York: Springer.
Bühler, K. (1907). Tatsachen und Probleme zu einer Psychologie der Denkvorgänge. Leipzig: Engelmann.
Köhler, W. (1925). The Mentality of Apes. London: Routledge & Kegan Paul
National Council of Teachers of Mathematics. (2000). Principles and Standards for School Mathematics. Reston, VA: National Council of Teachers of Mathematics.
Nguyen, D. T. (2025). Artificial intelligence (AI) in mathematics education: Bibliometric analysis for the period 2020-2025. International Electronic Journal of Mathematics Education, 20(4).